Visual Basic 5.0 Program: "VB Newton C"

The program VB Newton C uses the standard Newton's Law with a modification to simulate the movement of three objects written in Visual Basic 5.0. The C stands the speed of gravitational field.
Newton's Law assumes that the sum of all the forces of all objects is zero.
For the system to be in equilibrium the sum of all the forces on each object should be zero
To calculate these forces you can use the concept of gravitational field.
The gravitational field of an object with mass m is the force f(r) of a point mass 1 at a distance r.

f(r)= G*m/(r^2)

In the standard version Newton's Law assumes that the force acts instantaneous.
In the modified version this is not the case. That means the gravitaional field propagates through space with a speed c. For Newton's Law this means that in order to calculate the Force F(r) not the present distance is used but the past distance. That means the distance a time interval "t = r/c" in the past.
There are two ways implemented to calculate the past distance: Simple and Complex.

• In the simple way the past distance is calculated using the present postion and the previous position. The previous position meaning the position at the previous iteration.
• In the complex way the past distance is calculated using the present position and many previous positions. The previous position used is the time interval "t" divided by dt. This number is stored in the parameters van resp t 21 and t 31 in the Control Display.

The results of the simulations show that the difference between the two is very small.

Two three body simulations are implemented: 2 Black holes and planet Mercury simulation.

VB Program: "VB Newton C" Operation

The program uses three display or forms: Control Display, Simulation Display and Time Evolution Display

Control Display

The Control Display contains the following parameters which can be changed: Choice This parameter contains the name of simulation. Either "2 BH's" or "Mercury". The name changes when the parameter is selected. n object This parameters contains the number of objects in the simulation. The standard value is 3. Mass 1 This parameter contains the mass of object 1. The value is initialised when a new simulation is selected. The same for Mass 2 and Mass 3 Iteration This parameter contains the number of iterations for each simulation. The parameter is initialised when a new simulation is selected. c speed of gravitational field Prediction 0 = simple 1 = complex Vx Speed of Mass 1 in x direction. Vy Speed of Mass 1 in y direction.

The Control Display contains the following parameters which should not be changed:

• Active This parameter contains the active number of iterations.
• r m(2) radius of circle of object 2.
• r m(3) radius of circle of object 3.
• dt step size of each iteration.
• t 21 This is the value of the time interval "t" divided by dt calculated based on the distance between object 1 and object 2.
• t 31 The same as t 21 but between object 1 and object 3.

Each simulation is controlled by three Commands:

• "Calculate" This Command is used to start the simulation.
• "Stop" This Command is used to stop the simulation. This command is only vissible after the "Calculate" command is selected and active.
• "End" This Command is used to End the Visual Basic program. This command is only vissible when the "Calculate" command is not active.

Simulation Display

Time Evolution Display

The Time Evolution Display shows the evolution of a selected parameter or function in time. The parameter displayed depents on the type of simulation in progress
The Time Evolution Display shows the following Command:

• Clear This Command is used to clear the Simulation Display

The Time Evolution Display shows the following parameters which can be changed;

• Color This parameter shows the active color to control the displayed curve. The Time Evolution Display shows the following parameters which should not be changed. The parameters are only shown for the "Mecury" simulation.
• a and b Those two parameters define the function f(t)= a + b*t.
  This function is calculated using a leased squared average error function with the forward moving angle of the planet Mercury.

2 Black hole simulation

The 2 Black hole simulation contains 3 objects.

• The objects 1 and 2 are two Black holes of equal mass which rotate around each other.
  The radius of the circle for both is the parameter r m(2)
• Object 3 is a small object which rotates around the center of gravity of the two black holes.
  The radius of the circle is the parameter r m(3)

In order to observe the influence of a moving gravitational field perform the next steps;

1. • Set the parameter Choice to "2 BH's". This will initialize the other parameters.
   • set parameter n objects to 2.
   • Parameter c speed of gravitational field should be zero.
   • Select Calculate and observe "Simulation Display" and "Time Evolution display"

   The "Time Evolution display" with 2 objects shows the radius of object 1. The line is straight that means the radius of Black hole #1 (and also of #2) is constant. The system is stable.

2. • set parameter n objects to 3.
   • Select Calculate and observe "Time Evolution display"
   The "Time Evolution display" with 3 objects shows the distance of object 3 from its "average" value. The line shows a symetric wobble. The system is stable.
   The horizontal line shows the radius of object 1. In this case it is constant.
3. In order to demonstrate the influence of the speed of the gravitational field of the two blackholes perform the next 4 simulations:

   c vx vy color 0 0 0 0 50000 0 0 2 50000 1 1 4 50000 5 5 12

   Time Evolution Display

   Observe the right hand side of this display. You will observe a wobbly black line and three wobblied coloured lines. The three coloured lines are stacked. One above each other. They are shifted to the right compared to the black lines.

   • When you observe the horizontal line you will see that when c = 0 the line is horizontal and for c = 50000 slowly increases. That means the average distance between the Black holes slowly increases. This increase is independent of vx and vy.
   • When you observe the wobbled lines go to the right hand side or final end of the "Time evolution display". The black line shows c = 0 and the three coloured line c = 50000. When you observe the three coloured line carefully than you can observe that they are "stacked". Vx/vy = 5 is at the top and vx/vy = 0 is at the bottom. They are all slightly shifted towards the right compared to black line with c = 0
   • This right shift is caused because the radius of the third object increases as a result of an increase in the distance between the two black holes. This increase is comparable with an increase in wave length of the wobbles.
4. In order to learn more about the influence of the speed of the gravitational field of the two blackholes perform the same 4 simulations as previous but now with both vx and vy equal to 0, -1 and -5.

   When you compare the horizontal line for c = 50000 than there is no difference. The increase is independent of vx and vy. When you observe the wobbled lines go to the final end of the "Time evolution display". The black line shows c = 0 and is the same. The green line for c = 50000 and vx and vy = 0 are the same. The two coloured line c = 50000 for vx and vy both equal to -1 and -5 are different. The lines are "stacked". Vx/vy = -5 is now at the bottom and vx/vy = 0 is at the top. They are all slightly shifted towards the right compared to black line with c = 0. This shift is the same.

   Time Evolution Display

5. Next perform the same simulations but with the following combinations of vx and vy (c = 50000):

   (5,0) (-5,0), (0,5) (0,-5), (5,5) and (-5,-5).

   The combination (5,5) shows the higest combination at the end.
   The combination (-5,-5) shows the lowest combination at the end.
   

6. Next perform the same simulations but with the following combinations of vx and vy (c = 20000):

   (5,0) (-5,0), (0,5) (0,-5), (5,5) and (-5,-5).

   The wobbles are more pronounced.

The overal impression is that the trajectories of the third planet will be highly influenced by the speed and the common direction of the gravitational field which will make it very difficult to perform a realistic simulation based on actual observations when Black holes are involved.

Planet Mercury type simulation

The Planet Mercury type simulation contains 3 objects.

• Object 1 is a heavy object. Its is our Sun.
• Object 2 is a small object which rotates around the Sun. The path is an ellipse. This object represents the planet Mercury.
  The maximum distance (aphelion) is the parameter r m(2). Eccentricity is 0.6
• Object 3 is a small object which rotates in a circle around the Sun. This object represents the planet Jupiter.
  The radius of the circle around the Sun is the parameter r m(3)

The purpose of the test is to demonstrate of what is called the perihelion shift of the planet Mercury .

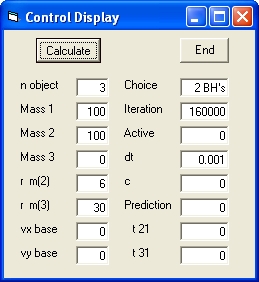
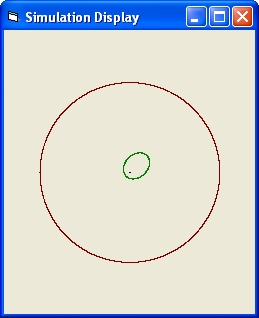
In order to test the program: Set the parameter Choice to "Mercury". This initialises all the parameters. Select "Calculate" and wait until the simulation is finished. Set parameter c Speed of gravitional field to 50000 and Select "Calculate" Set parameter vx to 1 and Select "Calculate" Simulation Display The simulation Display shows. One Black dot which is the Sun. A green trajectory, which is the planet Mercury. a brown circle, which is Jupiter

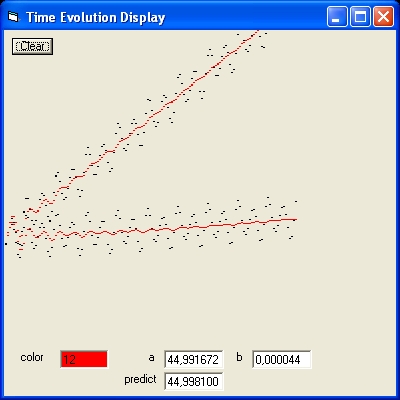
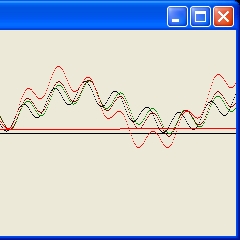
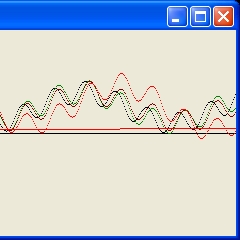
Time Evolution Display The Time Evolution Display shows three simulations. The top part shows the two cases with vx = 0. This is the sloping "line" The bottom part shows the case with vx = 1. This is the horizontal "line" The black dots represent what is observed i.e. the angle when Mercury reaches its maximum value after each revolution. The red dots represent a running average value of the angle. The function calculated is f(t) = a + b*t. The parameter a is the initial angle. The parameter b is the forward angle per time unit.

• When you perform the above test with n = 2 and c = 0 then whatever value you use for vx and vy the value of b = -0,000416.
  When you perform the above test with n = 3 and c = 0 then whatever value you use for vx and vy the value of b = 0,000539.
  The difference between the two, that means the difference between 0,000539 - (-0,000416) = 0,000955 is the forward movement of the aphelion single caused by object 3 i.e. the planet Mercury.

In order to demonstrate the advancement 9 tests are performed.
Each test consists of the next steps.

• Set the parameter Choice to "Mercury". This initialises all the parameters.
• set parameter n objects to 2 or to 3.
• Set parameter c Speed of gravitional field to 50000.
• set parameter Vx to 1, 0 or -1.
• set parameter Vy to 1, 0 or -1.
• Set parameter Color on Simulation Display.
• Select "Clear" Command. This is an option.

1. Table 1 is calculated with c = 50000 for n= 2.

   vy vx -1 0 1 1 -0,000431 -0.000943 -0,001458 0 0,000097 -0,000416 -0,000930 -1 0,000626 0,000113 -0,000408

   Table 1

2. Table 2 is calculated with c = 50000 for n= 3.

   vy vx -1 0 1 1 0.000480 -0.000011 -0,000504 0 0,001029 0,000539 0,000046 -1 0,001580 0,001089 0,000596

   Table 2

   The result with the situations 0,000539 and 0,000046 are shown above.
3. Table 3 shows what happens if you subtract 0.00539 from table 2.
   This is the value in the center of the table with both vx=0 and vy=0

   vy vx -1 0 1 1 -0.000059 -0.000550 -0,001043 0 0,000490 0 -,000495 -1 0,001041 0,000550 0,000057

   Table 3

   What Table 3 shows is that the largest forward movement of the planet Mercury is observed when the whole system moves in the "vx" = -1 and "vy" = -1. That is parallel with the long axis of the ellipse of the planet Mercury when the planet moves towards the Sun.
   To observe that change the parameter dt from 0.001 to 0.0001 and select "Calculate".
   This forward angle increases linear when the speed increases
   To observe this and try for both speads vx/vy -1,-2 and -3
   • With n=2 the angle increases from 0,000626 to 0,001668 to 0,002711
     
   • With n=3 the angle increases from 0,001580 to 0,002622 to 0,003664
     

---

VB Program: VB Newton C.bas source

In order to get the Visual Basic 5.0 source and the executable program use the following zip file:VB Newton C.zip
The Zip files contains the following 6 files:

• (1) VB Newton C.vbp (2) VB Newton C.vbw (3) VB VB Newton C.frm (4) VB Newton C Display.frm (5) VB Newton C.bas and (6) VB Newton C.exe

The Visual Basic Executable program requires MSVDVM50.DLL: Msvdvm50.dll.zip

Reflection Black Holes

The most difficult calculation to perform is the two Black hole simulation based on actual observations. In order to do that you first have to calculate the masses of both black holes based on observations. That means (and this is a real tough point) you can only use the observations of stars which revolve around the two black holes, but not the positions of the blackholes them self because they cannot be observed. What this means that it is very difficult to calculate the masses and the individual positions of each Black hole which in turn makes it very difficult to make acurate predictions of the positions of the third object.
This same problem exists as part of the LISA: Laser Interferometer Space Antenna (NASA) project which tries to detect gravitational waves by means of studying the collision of Black Holes. See also: Gravitational Waves and Massive Black Holes? – The LISA and LISA Pathfinder Missions
IMO the chance of succes are extremely bleak.

Part of the problem is that the Black holes are there already during the start of the observations which makes it extremely difficult to calculate the the initial conditions of the simulations based on actual observations (which are partly invisible). This is a difficult problem when your system is stable but extremely complex when your system is unstable i.e when the black holes will collide.

Reflection Mercury

The forward movement of Mercury is controlled by three physical concepts:

(1) The other planets, (2) The movement of the Sun through/around our Galaxy and (3) The propagation or speed of gravitational field

The advantage of this example is that all objects are visible and easy to observe (over a long range of time) which makes accurate predictions rather simple. The biggest problem is the speed of the gravitational field and/or the speed of the gravitons. Photons move with the speed of the electro/magnetic field which is c. To claim to the speed of gravitons is physical identical as the speed of photons could be misleading because IMO the two are different. This becomes clear when you consider that a gravitational field changes the path of photons. IMO the reverse is not true.

Reflection: How black are Black Holes.

Black Holes are not completely black. Of course to call very massive compact objects black is a wrong conceptbecause it is based on a human quality. Namely that we have eyes which are detectors of light specific photons.
In general photons are part of what is called electro magnetic radiation which are photons of all different frequencies and energy's
The issue is that a massive compact object becomes "invisible" when the photon energy becomes smaller as the escape velocity of photons in the frequency range of visible light.

The reason why they are not completely black is because they can be detected by means of the gravitational field or better the emission of gravitons which influences the behaviour of rotating objects
When you have two rotating Black holes this dynamic field causes what are called gravitational waves and the wobbling of the trajectories of the rotating objects.

Feedback

No feedback received.

Back to Celestial mechanics for dummies?
Back to my home page Contents of This Document